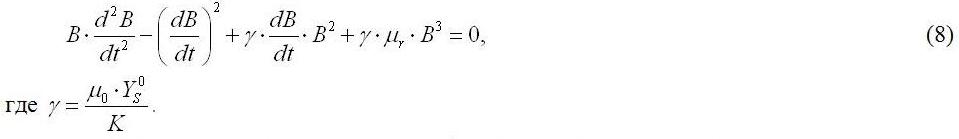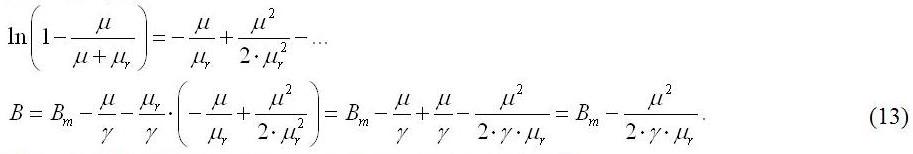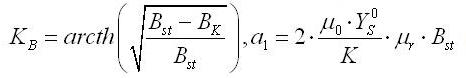|
 |
|
Динамическая модель субстратзависимого роста накопительной культуры микроводорослей
Лелеков А.С.1, Геворгиз Р. Г.2, Гаврилов П. Е.1 Alexander S. Lelekov1, Ruslan G. Gevorgiz2, Petr E. Gavrilov1
1Севастопольский государственный университет
УДК 519.876:582.26/27
Предложена модель динамики плотности непроточной по лимитирующему субстрату накопительной культуры микроводорослей. Модель основана на предположении о том, что наблюдаемая скорость роста есть разность скоростей биосинтеза и потерь биомассы, зависимость между удельной скоростью роста и концентрацией лимитирующего субстрата выбрана в виде ломаной. Получены зависимости продуктивности и удельной скорости роста от плотности культуры, а также аналитическое выражение динамики субстратзависимого роста накопительной культуры, лимитированной одним из минеральных компонентов среды, в виде гиперболического тангенса. Ключевые слова: математическая модель; накопительная культура микроводорослей; удельная скорость роста; продуктивность.
Введение. Культура микроводорослей широко используется в качестве модельного объекта в гидроэкологии (Тренкеншу, 2009). Основной характеристикой роста культуры микроводорослей в заданных условиях является накопительная кривая. По форме накопительной кривой можно определить факторы, ограничивающие продуктивность в той или иной фазе роста. В связи с этим, при работе с накопительной культурой микроводорослей важно произвести корректную математическую обработку полученных экспериментальных данных. Классические математические модели роста микроводорослей в накопительной культуре основываются на представлениях субстрат-зависимого роста по аналогии с ферментативной кинетикой: модель Моно (Monod, 1949), логистическая функция Ферхюльста-Пирля (Вальтер, Лампрехт, 1976), либо их производные (Иерусалимский, Неронова, 1965; Droop, 1973). В современных работах динамические модели роста биомассы также основаны на представлениях Моно (Mairet et al., 2011; Zhou et al., 2014). В некоторых случаях экспериментальные данные описываются логистической функцией (Yang et al., 2011) или полином (Costa et al., 2002). Указанные математические модели широко применяются при исследовании влияния различных факторов среды на рост проточных культур (Flynn, 2001), а также используются при математическом описании накопления биологически ценных веществ (Luedeking, Piret, 2000; Tevatia, Demirel, Blum, 2011). Для проточных культур микроводорослей использование уравнения Моно позволяет описать данные с высокой точностью (Zhou et al., 2014), но применение его для накопительной культуры требует некоторых оговорок. В процессе накопительного роста культуры (особенно для плотных культур) клетки микроводорослей постоянно адаптируются к изменяющимся условиям, при этом биохимический состав биомассы может варьировать в широких пределах (Fresnedo, 1992; Gatenby et. al., 2003; Тorzillo et. al., 2012). Следовательно, уравнения, основанные на представлениях Моно, не применимы для описания всей накопительной кривой. В целом, довольно ограниченное число теоретических работ при моделировании динамики роста накопительной культуры связано с тем, что решения дифференциальных уравнений для нестационарного процесса трудно представить в элементарных аналитических функциях. В предыдущей работе нами предложены математические модели роста накопительной культуры микроводорослей для условия закрытой по лимитирующему субстрату системы (Геворгиз, Лелеков, Король, 2013). Показано, что накопительную кривую в общем виде нельзя описать одним уравнением, так как происходит смена лимитирующего фактора: 1. Можно выделить область, где рост ограничен внутренними особенностями данного объекта, при этом удельная скорость роста постоянна и максимальна, а мы имеем дело с экспоненциальным ростом; 2. Можно выделить область, где скорость роста зависит от внешней концентрации лимитирующего субстрата. Предложенная математическая модель для второй области является довольно упрощенной, так как не учитывает потерь биомассы за счет гибели клеток, «дыхания», выделения экзометаболитов во внешнюю среду и т. д. Цель данной работы – разработка динамической модели субстрат-зависимого роста культуры микроводорослей, непроточной по лимитирующему субстрату, основанной на предположении, что скорость роста культуры определяется разностью скоростей биосинтеза и потерь биомассы.
Результаты и обсуждение. Запишем зависимость удельной скорости роста культуры μ от концентрации лимитирующего субстрата в среде S в виде ломанной (Тренкеншу, 2010):
где μ0 – максимальная удельная скорость синтеза биомассы, μr – удельная скорость потерь биомассы, К – константа насыщения. Из (1) следует, что при постоянстве удельных скоростей синтеза и потерь, а также S ≥ K культура будет расти согласно экспоненциальному закону Мальтуса. Экспериментально доказано, что такой рост может продолжаться лишь ограниченный промежуток времени, который получил название «фазы экспоненциального роста». По её окончании, культура перейдёт в фазу замедления роста, при этом скорость роста будет зависеть от концентрации лимитирующего субстрата в культуральной среде. Кроме того, для малых концентраций субстрата (S < K) углы наклона всех вышеуказанных классических моделей субстрат-зависимого роста близки. Поэтому использование зависимости удельной скорости роста от концентрации субстрата в виде ломаной является целесообразным. Рассмотрим случай лимитирования роста культуры микроводорослей субстратом S (S < K):
В выражении (2) максимальную удельную скорость синтеза, удельную скорость потерь биомассы и константу насыщения будем считать постоянными видоспецифичными коэффициентами, которые можно определить экспериментально. Таким образом, при уменьшении концентрации лимитирующего субстрата в среде удельная скорость роста линейно снижается. Продифференцируем уравнение (2) по времени:
По определению, удельная скорость есть скорость роста единицы биомассы:
Теперь производная от удельной скорости роста по времени примет вид:
Для получения искомого решения биомассы от времени в уравнение (3) необходимо записать значение скорости изменения концентрации лимитирующего субстрата dS / dt. Будем считать, что скорость изменения концентрации лимитирующего субстрата в среде прямо пропорциональна скорости синтеза биомассы:
где По определению, скорость синтеза биомассы можно выразить через удельную скорость синтеза μS. В условиях поставленной задачи, удельная скорость синтеза биомассы будет изменяться, так как мы имеем дело с лимитированным ростом:
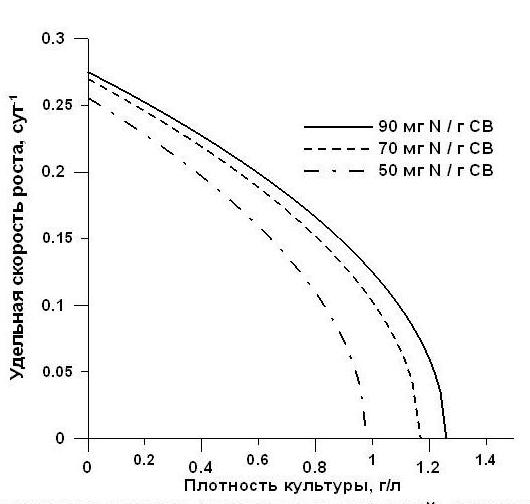
Балансовое уравнение (5) запишем в виде:
Подставляя выражения (4) и (7) в (3), получим дифференциальное уравнение зависимости плотности культуры от времени:
Для решения данного уравнения необходимо произвести замену:
По сути, уравнение (9) есть запись выражения для продуктивности (абсолютной скорости роста). Для нахождения второй производной по биомассе, продифференцируем (9) и подставим в (8):
Первое слагаемое правой части последнего выражения есть удельная скорость роста:
Подставим:
Разделяя переменные, интегрируем при начальных условиях μ = μm, B = Bk:
Рассмотрим граничное условие: при достижении культурой стационарной фазы роста, удельная скорость роста будет равняться нулю, а биомасса достигнет своего максимального значения B=Bst:
Для нахождения искомого решения зависимости биомассы от времени необходимо произвести обратные замены в (12) с последующим интегрированием полученных выражений. Однако зависимость (12) является трансцендентным уравнением, решение которого нельзя выразить в аналитическом виде, поэтому разложим (12) в ряд Тейлора в окрестностях нуля:
Выразим удельную скорость роста из последнего выражения:
Уравнение (14) применимо в случае лимитирования роста накопительной культуры микроводорослей одним из минеральных невозвратных компонентов питательной среды, причём диапазон изменения плотности культуры составляет от ВК до Bst, а удельной скорости роста – от μm до 0. Уравнение (14) показывает, что при лимитировании роста культуры удельная скорость роста уменьшается пропорционально корню квадратному от биомассы. На рис. 1 представлены типовые теоретические кривые зависимости удельной скорости роста от биомассы по (14) при различных значениях коэффициента истинной потребности. Значения неизвестных коэффициентов получены из работы (Дробецкая, Минюк, Тренкеншу и др., 2001), считая, что фаза лимитирования роста спирулины азотом началась с момента начала эксперимента. Величину удельной скорости потерь биомассы будем считать равной 0,1 сут-1. Приведённые графики показывают, что при увеличении истинной потребности клеток микроводорослей в лимитирующем биогенном элементе, удельная скорость роста культуры достигает нулевого значения при меньших величинах стационарной плотности накопительной культуры.
Рис. 1. Теоретические кривые зависимости удельной скорости роста от плотности культуры по уравнению (14) при различных величинах коэффициента истинной потребности.
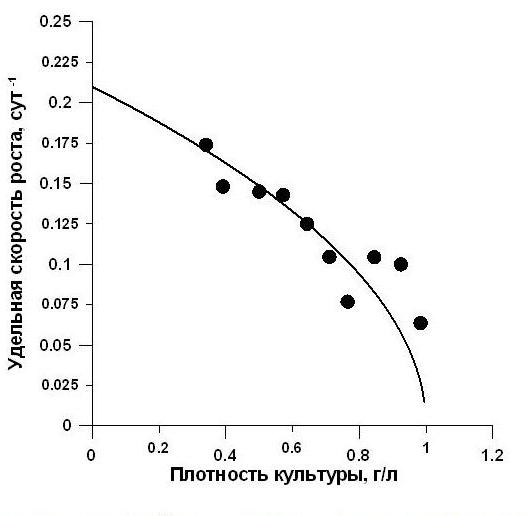
Подобные кривые зависимости удельной скорости роста от величины биомассы часто наблюдаются экспериментально. Например, на рис. 2 представлена зависимость удельной скорости роста спирулины от плотности культуры по тем же данным (Дробецкая, Минюк, Тренкеншу и др., 2001). Стоит отметить высокое соответствие теоретической кривой (14) и экспериментальных данных (R2 = 0,9). Аппроксимация экспериментальных данных уравнением (14) позволила определить обобщённый коэффициент подкоренного выражения, с помощью которого можно рассчитать значение коэффициента истинной потребности спирулины в азоте при известных µ0 и К (см. выше) – 50 мг N/ г СВ. Такое значение истинной потребности спирулины в азоте на 17 мг N/ г СВ ниже, чем рассчитанное по тем же данным в работе (Тренкеншу, Лелеков, 2005), что можно объяснить различными подходами при объяснении экспериментальных данных. В работе (Тренкеншу, Лелеков, 2005) на накопительной кривой выделялась фаза линейного роста, а (14) предполагает нелинейное замедление роста, вызванное лимитированием по минеральному азоту. Поэтому более верным является второй вариант, так как линейный рост можно объяснить только лимитированием газовым либо энергетическим потоком. Для уточнения значений расчётных коэффициентов необходимо проведение дополнительных экспериментов.
Рис. 2. Зависимость удельной скорости роста спирулины от плотности культуры по данным (Дробецкая, Минюк, Тренкеншу и др., 2001) при лимитировании роста нитратным азотом.
Для определения зависимости продуктивности от плотности культуры необходимо выполнить обратную подстановку, получаем уравнение для скорости роста:
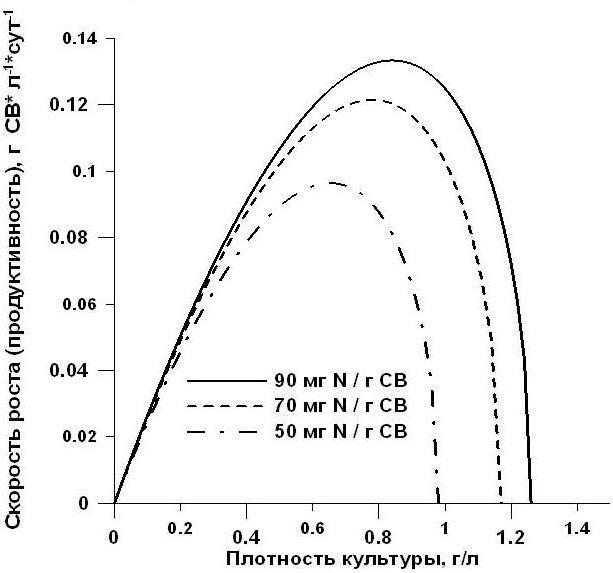
Уравнение (15) показывает зависимость абсолютной скорости роста культуры от величины её плотности. На рис. 3 данная зависимость представлена графически для различных значений коэффициента истинной потребности. При увеличении Ys0 мы наблюдаем более высокую максимальную продуктивность. Как и в случае с удельной скоростью роста (15) применимо только на участке лимитирования роста минеральным субстратом, причём диапазон изменения плотности культуры от ВК до Bst, а продуктивности от µm • ВК до 0.
Рис. 3. Теоретические кривые зависимости абсолютной скорости роста от плотности культуры по уравнению (15) при различных величинах коэффициента истинной потребности.
Теперь можно записать дифференциальное уравнение, описывающее изменение биомассы во времени:
Решение последнего уравнения с учетом двух обобщённых коэффициентов:
можно записать в виде:
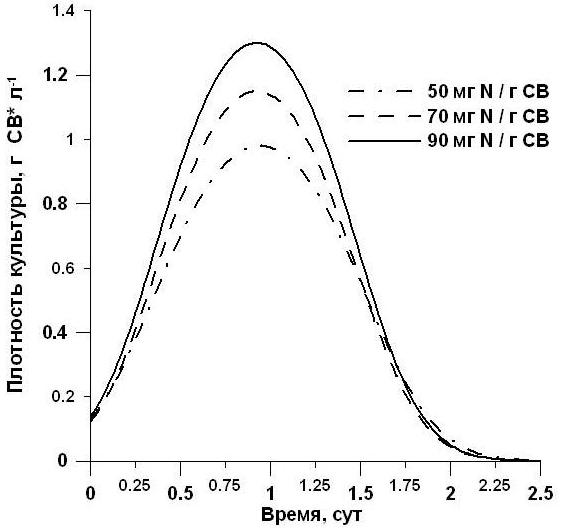
Уравнение (16) применимо для описания динамики плотности культур микроводорослей (в диапазоне от ВК до Вst) при лимитировании их роста пластическим субстратом, доля возврата которого в биосинтетические процессы близка нулю, либо время возврата достаточно велико. Например, таким пластическим субстратом может выступать минеральный азот в нитратной форме. На рис. 4 представлены типовые теоретические кривые зависимости плотности культуры от времени для различных значений коэффициента истинной потребности. Анализируя рис. 4, мы видим, что в соответствии с предложенной моделью и её математической записью в виде уравнения (16), плотность накопительной культуры увеличивается до максимального значения. Это обусловлено тем, что концентрация лимитирующего субстрата достигает компенсационного значения
Рис. 4. Теоретические кривые динамики плотности культуры микроводорослей по уравнению (16) при различных величинах коэффициента истинной потребности.
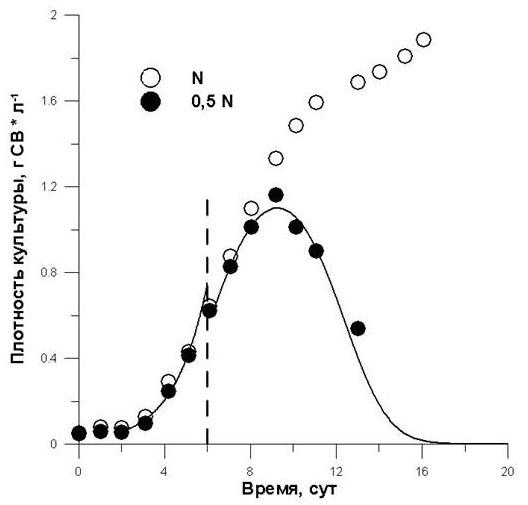
Полученная модель (16) применена при описании экспериментальных данных роста культуры A. platensis в условиях лимитирования азотом. В опытном варианте содержание азота было уменьшено в 2 раза по сравнению с контрольным. Полученные результаты представлены на рис. 5. Анализируя рисунок 5, можно отметить высокое соответствие предлагаемой модели с реальными экспериментальными данными (R2 = 0,93). Следует отметить, что уравнения экспоненциальной фазы и фазы лимитирования (16) не сходятся в одну точку: на графике мы наблюдаем «разрыв» примерно на шестые сутки. Это связано с тем, что эта точка соответствует моменту, когда концентрация лимитирующего субстрата (в данном случае азота) снижается до константы насыщения K. Именно в области этой концентрации уравнение зависимости μ(S) в виде ломанной хуже всего описывает экспериментальные данные. Кроме того, при переходе культуры из экспоненциальной в фазу лимитирования роста происходят изменения биохимического состава клеток микроводорослей.
Рис. 5. Накопительные кривые роста культуры A. platensis при различном начальном содержании нитратного азота в среде. Линии – аппроксимация фазы замедления роста уравнением (16). Пунктирная линия – момент начала лимитированного роста.
Заключение. Основной целью данной работы являлась разработка математической модели субстрат-зависимого роста накопительной культуры микроводорослей. Полученные результаты являются продолжением предыдущих исследований роста культур микроводорослей в условиях закрытой по лимитирующему субстрату системы. Однако, в отличие от ранее предложенных моделей, в данной работе мы учли убыль биомассы микроводорослей за счёт потерь клеточных структур при делении, экскреции метаболитов, темнового дыхания и пр. Основным достоинством предложенной модели является наличие аналитического решения, что значительно упрощает математическую обработку экспериментальных данных и позволит получить новые знания о росте накопительной культуры микроводорослей.
Благодарности. Работа выполнена в рамках Государственного заказа на исследования (N2015/702)
Список литературы 1. Белянин В. Н. Светозависимый рост низших фототрофов (в управляемых условиях). – Новосибирск: Наука, 1984. – 96 с. 2. Вальтер Р., Лампрехт И. Современные теории и уравнения роста / Термодинамика биологических процессов. – М.: Наука, 1976. – С. 98-112. 3. Геворгиз Р. Г., Лелеков А. С., Король О. Н. Моделирование динамики роста популяции микроорганизмов в накопительной культуре. Закрытая система // Рыбное хозяйство Украины. 2013. Т. 5. С. 6-15. 4. Дробецкая И. В., Минюк Г. С., Тренкеншу Р. П. и др. Ростовые и биохимические характеристики Spirulina platensis (Nordst.) Geitler при различных условиях минерального питания // Экология моря. 2001. 56. С. 41-46. 5. Иерусалимский Н. Д., Неронова Н. М. Количественная зависимость между концентрацией продуктов обмена и скоростью роста микроорганизмов // ДАН СССР. 1965. 161. С. 1437. 6. Лелеков А. С., Геворгиз Р. Г. Динамика плотности культуры микроводорослей в стационарной фазе роста // Бюлетень ГНБС. 2013. 108. С. 39-44. 7. Тренкеншу Р. П., Лелеков А. С. Простейшие модели роста микроводорослей. 3. Потребность микроводорослей в элементах минерального питания // Экология моря. 2005. 70. С. 53-61. 8. Тренкеншу Р. П. Кинетика субстратзависимых реакций при различной организации метаболических систем. – Севастополь: ЭКОСИ-Гидрофизика, 2005. – 89 с. 9. Тренкеншу Р. П. Простейшие модели роста микроводорослей. 6. Предельные скорости роста // Экология моря. 2010. 80. С. 85-91. 10. Филипповский Ю. Н. Анализ математических моделей фотосинтезирующих систем и некоторые вопросы фитооблучения: автореф. дис. .... канд. биол. наук. – М., 1970. – 25 с. 11. Baly E. C. C. The kinetics of photosynthesis // Proc. R. Soc. Lond. 1935. 117. P. 218-239. 12. Blackman F. F. Optima and limiting factors // Ann. Bot. Lond. 1905. 19. P. 281-295. 13. Costa J. A., Colla L. M., Filho P. D., Kabke K., Weber A. Modelling of Spirulina platensis growth in fresh water using response surface methodology // World J. of Microb. & Biotech. 2002. 18. P. 603-607. 14. Droop M. R. Some thoughts on nutrient limitation in algae // J. Phycol. 1973. 9. P. 264-272. 15. Flynn K. J. A mechanistic model for describing dynamic multi-nutrient, light, temperature iteraction in phytoplankton // J. Plan. Res. 2001. 23. P. 977-997. 16. Fresnedo O., Serra J. L. Effect of nitrogen starvation on the biochemistry of Phormidium laminosum (Сyanophyceae) // J. Phycol. 1992. 28. P. 786-793. 17. Gatenby C. M., Orcutt D. M., Kreeger D. A., Parker B. C., Jones V. A., Neves R. G. Biochemical composition of three algal species proposed as food for captive freshwater mussels // J. Appl. Phycol. 2003. 15. P. 1-11. 18. Geider R. J., MacIntyre H. L., Kana T. M. A dynamic model of photoadaptation in phytoplankton // Limnol. Oceanogr. 1996. 41, № 1. P. 1-15. 19. Gorski F. The equation of the light curve of photosynthesis. //Act. Biol. Crac. 1961. 3. P. 75-83. 20. Jassby A. D., Platt T. Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. // Limn. Ocean. 1976. 21, № 4. P. 540-547. 21. Mairet F., Bernard O., Masci P. et. al. Modelling neutral lipid production by the microalga Isochrysis galbana under nitrogen limitation // Bioresource Technology. 2011. 102. P.142-149. 22. Luedeking R., Piret E. L. A kinetic study of the lactic acid fermentation. Batch process at controlled pH // Biotechnology and Bioengineering. 2000. 67. P. 636-644. 23. Monod J. The growth of bacterial cultures // Ann. Rev. Microbiol. 1949. 3. P. 371-394. 24. Tevatia R., Demirel Y., Blum P. Kinetic modeling of photoautotropic growth and neutral lipid accumulation in terms of ammonium concentration in Chlamydomonas reinhardtii // Bioresource Technology. 2012 .119. P.419-424. 25. Тorzillo G., Faraloni C., Silva A. et al. Photoacclimation of Phaeodactylum tricornutum (Bacillariophyceae) cultures grown outdoors in photobioreactors and open ponds // Eur. J. Phycol. 2012. 47, № 2. Р. 169-181. 26. Zhou X. et al. Modelling microalgae growth in nitrogen-limited continuous culture // Energy (2014), http://dx.doi.org/10.1016/j.energy.2014.06.058 27. Yang J., Rasa E., Tantayotai P. et. al. Mathematical model of Chlorella minutissima UTEX2341 growth and lipid production under photoheterotrophic fermentation conditions // Bioresource Technology. 2011. 102. P. 3077-3082. Статья поступила в редакцию 25.05.2016 Dynamic model substrate-dependent growth of microalgae butch culture A.S. Lelekov, R.G. Gevorgiz, P.E. Gavrilov The dynamic model substrate-dependent growth of microalgae butch culture is presented. The model have been based on the assumption that observable growth rate is a difference of synthesis rate and biomass loss rate. The rate of limiting substrate return from the broken up biomass presumably is equal to zero. The analytical equation of productivity and specific growth rate from biomass are obtained. The dynamic substrate-dependent growth of microalgae butch culture in form hyperbolic tangent is received. Об авторах Лелеков Александр Сергеевич - Lelekov Alexander Sergeevich кандидат биологических наук a.lelekov@yandex.ru Геворгиз Руслан Георгиевич - Gevorgiz Ruslan Georgievich кандидат биологических наук r-gevorgiz@yandex.ru Гаврилов Петр Евгеньевич - Gavrilov Petr Evgenievich аспирант Корреспондентский адрес: Россия, 299011, Севастополь, пр. Нахимова, 2, ФГБУН ИМБИ, Отдел биотехнологий и фиторесурсов; тел. 88692550795. ССЫЛКА НА СТАТЬЮ: Лелеков А.С., Геворгиз Р.Г., Гаврилов П.Е. Динамическая модель субстратзависимого роста накопительной культуры микроводорослей // Вопросы современной альгологии. 2016. № 2 (12). URL: http://algology.ru/970 Уважаемые коллеги! Если Вы хотите получить версию статьи в формате PDF, пожалуйста, напишите в редакцию, и мы ее вам с удовольствием пришлем бесплатно. При перепечатке ссылка на сайт обязательна
На ГЛАВНУЮ
|
|
|
 | | ||
|
| ||
– истинная потребность клеток в лимитирующем субстрате – количество лимитирующего субстрата необходимое для синтеза единицы биомассы. При дальнейших расчётах будем считать значение истинной потребности величиной постоянной. Такое предположение является довольно упрощённым, так как известно, что при лимитировании роста культуры микроводорослей одним из биогенных элементов происходит изменение биохимического состава клеток (Fresnedo, 1992; Gatenby et. al., 2003; Тorzillo et. al., 2012). Однако в том случае, если клетки микроводорослей адаптированы к малым концентрациям субстрата, то значительного изменения биохимического состава культуры не происходит.
, при этом наблюдаемая скорость роста равна нулю. В следующий момент времени процессы деструкции биомассы преобладают над синтезом, что приводит к снижению плотности культуры. Культура переходит в фазу отмирания, что на графике представлено уменьшением биомассы вплоть до нулевого значения. Однако предлагаемая модель базируется на предположении о полной потере субстрата, который выделяется из распавшейся биомассы. В случае если происходит возврат лимитирующего субстрата, на фазе отмирания будут наблюдаться колебания плотности культуры (Лелеков, Геворгиз, 2013), период которых определяется временем возврата, а предложенная модель не применима.
